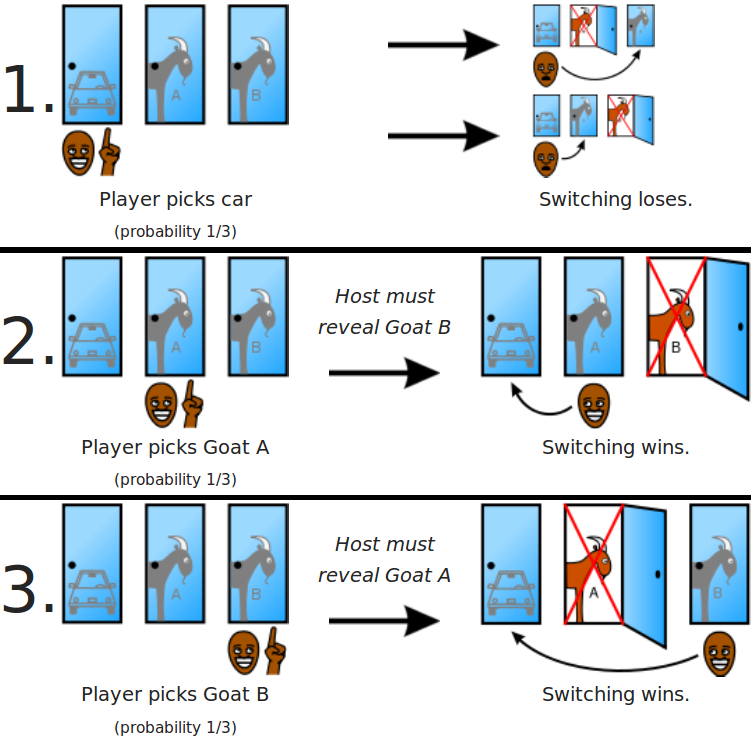
The monty hall problem is a popular math probability puzzle. The game consist of three closed doors, two of which contain goat inside them and one contains a car (or anything precious). You are given a chance to select one of the three doors. After you make your selection, the host opens one of the doors from the two remaining doors and shows you a goat in that door. After this, should you change your selection?
It can seem a useless act to switch the door because it looks like 50/50 change of having car in any of the two doors. But actually, if you switch the door, your chance of winning the car increases to 66% while if you don’t switch the door, it will remain 33%. It can be clear from the image below.
This small python program simulates the monty hall problem. The greater number of times you play, the closer your success percentage will reach to 66.66%.
#!/usr/bin/python
from random import randrange
print "Monty Hall Simulator"
simnum = int(input("How many simulations to run?"))
changepoint = 0
nochangepoint = 0
for j in range(0, simnum):
# generate a random number (1 to 3)
a = randrange(1, 4)
# choose a door
choice = randrange(1, 4)
# choose a door to show
showdoor = randrange(1, 4)
# the door we show must not be the door the player selected
# or the door that contains the prize
while showdoor == choice or showdoor == a:
showdoor = randrange(1, 4)
# second choice represent that the player chose another door
secondchoice = 1
while secondchoice == choice or secondchoice == showdoor:
secondchoice = randrange(1, 4)
# if the first choice was the winning door, add to nochangepoint. Else,
# add to changepoint
if a == choice:
nochangepoint += 1
else:
changepoint += 1
print "In total ", simnum, " games, the player will win ", changepoint, " rounds if he switches the door. Else, he wins ", nochangepoint, " rounds"
print "In percentage, win rate is ", ((changepoint / (simnum*1.0)) * 100), " % for switching and ", ((nochangepoint / (simnum*1.0))*100), " % for not switching"